
摘要: 在本文中,我想带领大家看一看最近在Keras中实现的体系结构中一系列重要的卷积组块。
作为一名计算机科学家,我经常在翻阅科学技术资料或者公式的数学符号时碰壁。我发现通过简单的代码来理解要容易得多。因此,在本文中,我想带领大家看一看最近在Keras中实现的体系结构中一系列重要的卷积组块。
当你在网站上寻找常用架构实现时,一定会对它们里面的代码量感到惊讶。如果标有足够多的注释并使用额外的参数来改善模型,将会是一个非常好的做法,但与此同时这也会分散体系结构的本质。为了进一步简化和缩短代码,我将使用一些别名函数:
defconv(x, f, k=3, s=1, p='same', d=1, a='relu'): return Conv2D(filters=f, kernel_size=k, strides=s, padding=p, dilation_rate=d, activation=a)(x)def dense(x, f, a='relu'): return Dense(f, activation=a)(x)defmaxpool(x, k=2, s=2, p='same'): return MaxPooling2D(pool_size=k, strides=s, padding=p)(x)defavgpool(x, k=2, s=2, p='same'): return AveragePooling2D(pool_size=k, strides=s, padding=p)(x)defgavgpool(x): return GlobalAveragePooling2D()(x)defsepconv(x, f, k=3, s=1, p='same', d=1, a='relu'): return SeparableConv2D(filters=f, kernel_size=k, strides=s, padding=p, dilation_rate=d, activation=a)(x)
在删除模板代码之后的代码更易读。当然,这只有在你理解我的首字母缩写后才有效。
defconv(x, f, k=3, s=1, p='same', d=1, a='relu'): return Conv2D(filters=f, kernel_size=k, strides=s, padding=p, dilation_rate=d, activation=a)(x)def dense(x, f, a='relu'): return Dense(f, activation=a)(x)defmaxpool(x, k=2, s=2, p='same'): return MaxPooling2D(pool_size=k, strides=s, padding=p)(x)defavgpool(x, k=2, s=2, p='same'): return AveragePooling2D(pool_size=k, strides=s, padding=p)(x)defgavgpool(x): return GlobalAveragePooling2D()(x)defsepconv(x, f, k=3, s=1, p='same', d=1, a='relu'): return SeparableConv2D(filters=f, kernel_size=k, strides=s, padding=p, dilation_rate=d, activation=a)(x)
瓶颈(Bottleneck)组块
一个卷积层的参数数量取决于卷积核的大小、输入过滤器的数量和输出过滤器的数量。你的网络越宽,3x3卷积耗费的成本就越大。
def bottleneck(x, f=32, r=4): x = conv(x, f//r, k=1) x = conv(x, f//r, k=3) return conv(x, f, k=1)
瓶颈组块背后的思想是,使用一个低成本的1x1卷积,按照一定比率r将通道的数量降低,以便随后的3x3卷积具有更少的参数。最后,我们用另外一个1x1的卷积来拓宽网络。
Inception模块
模块提出了通过并行的方式使用不同的操作并且合并结果的思想。通过这种方式网络可以学习不同类型的过滤器。
defnaive_inception_module(x, f=32): a = conv(x, f, k=1) b = conv(x, f, k=3) c = conv(x, f, k=5) d = maxpool(x, k=3, s=1) return concatenate([a, b, c, d])
在这里,我们将使用卷积核大小分别为1、3和5的卷积层与一个MaxPooling层进行合并。这段代码显示了Inception模块的原始实现。实际的实现结合了上述的瓶颈组块思想,这使它稍微的复杂了一些。
definception_module(x, f=32, r=4): a = conv(x, f, k=1) b = conv(x, f//3, k=1) b = conv(b, f, k=3) c = conv(x, f//r, k=1) c = conv(c, f, k=5) d = maxpool(x, k=3, s=1) d = conv(d, f, k=1) return concatenate([a, b, c, d])
Inception模块
剩余组块(ResNet)
ResNet是由微软的研究人员提出的一种体系结构,它允许神经网络具有任意多的层数,同时还提高了模型的准确度。现在你可能已经习惯使用它了,但在ResNet之前,情况并非如此。
defresidual_block(x, f=32, r=4): m = conv(x, f//r, k=1) m = conv(m, f//r, k=3) m = conv(m, f, k=1) return add([x, m])
ResNet的思路是将初始的激活添加到卷积组块的输出结果中。利用这种方式,网络可以通过学习过程决定用于输出的新卷积的数量。值得注意的是,Inception模块连接这些输出,而剩余组块是用于求和。
ResNeXt组块
根据它的名称,你可以猜到ResNeXt与ResNet是密切相关的。作者们将术语“基数(cardinality)”引入到卷积组块中,作为另一个维度,如宽度(通道数量)和深度(网络层数)。
基数是指在组块中出现的并行路径的数量。这听起来类似于以并行的方式出现的4个操作为特征的Inception模块。然而,基数4不是指的是并行使用不同类型的操作,而是简单地使用相同的操作4次。
它们做的是同样的事情,那么为什么你还要把它们并行放在一起呢?这个问题问得好。这个概念也被称为分组卷积,可以追溯到最早的AlexNet论文。尽管当时它主要用于将训练过程划分到多个GPU上,而ResNeXt则使用ResNeXt来提高参数的效率。
defresnext_block(x, f=32, r=2, c=4): l = [] for i in range(c): m = conv(x, f//(c*r), k=1) m = conv(m, f//(c*r), k=3) m = conv(m, f, k=1)l.append(m) m = add(l) return add([x, m])
这个想法是把所有的输入通道分成一些组。卷积将只会在其专用的通道组内进行操作,而不会影响其它的。结果发现,每组在提高权重效率的同时,将会学习不同类型的特征。
想象一个瓶颈组块,它首先使用一个为4的压缩率将256个输入通道减少到64个,然后将它们再恢复到256个通道作为输出。如果想引入为32的基数和2的压缩率,那么我们将使用并行的32个1x1的卷积层,并且每个卷积层的输出通道是4(256/(32*2))个。随后,我们将使用32个具有4个输出通道的3x3的卷积层,然后是32个1x1的卷积层,每个层则有256个输出通道。最后一步包括添加这32条并行路径,在为了创建剩余连接而添加初始输入之前,这些路径会为我们提供一个输出。
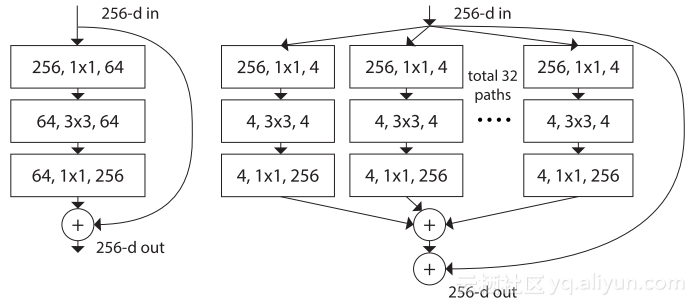
左侧: ResNet组块 右侧: 参数复杂度大致相同的RexNeXt组块
这有不少的东西需要消化。用上图可以非常直观地了解都发生了什么,并且可以通过复制这些代码在Keras中自己创建一个小型网络。利用上面9行简单的代码可以概括出这些复杂的描述,这难道不是很好吗?
顺便提一下,如果基数与通道的数量相同,我们就会得到一个叫做深度可分卷积(depthwise separable convolution)的东西。自从引入了Xception体系结构以来,这些技术得到了广泛的应用。
密集(Dense)组块
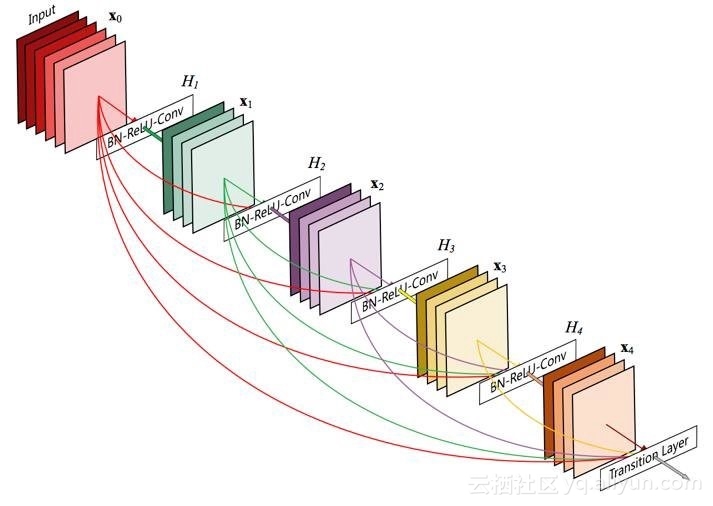
密集组块是剩余组块的极端版本,其中每个卷积层获得组块中之前所有卷积层的输出。我们将输入激活添加到一个列表中,然后输入一个可以遍历块深度的循环。每个卷积输出还会连接到这个列表,以便后续迭代获得越来越多的输入特征映射。这个方案直到达到了所需要的深度才会停止。
defdense_block(x, f=32, d=5): l = x for i in range(d): x = conv(l, f) l = concatenate([l, x]) return l
尽管需要数月的研究才能得到一个像DenseNet这样出色的体系结构,但是实际的构建组块其实就这么简单。
SENet(Squeeze-and-Excitation)组块
SENet曾经在短期内代表着ImageNet的较高水平。它是建立在ResNext的基础之上的,主要针对网络通道信息的建模。在常规的卷积层中,每个通道对于点积计算中的加法操作具有相同的权重。
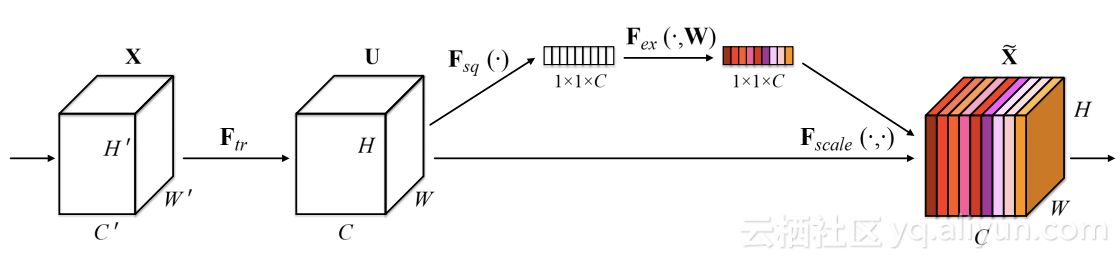
Squeezeand Excitation组块
SENet引入了一个非常简单的模块,可以添加到任何现有的体系结构中。它创建了一个微型神经网络,学习如何根据输入对每个过滤器进行加权。正如你看到的那样,SENet本身不是一个卷积组块,但是因为它可以被添加到任何卷积组块中,并且可能会提高它的性能,因此我想将它添加到混合体中。
defse_block(x, f, rate=16): m = gavgpool(x) m = dense(m, f // rate) m = dense(m, f, a='sigmoid') return multiply([x, m])
每个通道被压缩为一个单值,并被馈送到一个两层的神经网络里。根据通道的分布情况,这个网络将根据通道的重要性来学习对其进行加权。最后,再用这个权重跟卷积激活相乘。
SENets只用了很小的计算开销,同时还可能会改进卷积模型。在我看来,这个组块并没有得到应有的重视。
NASNet标准单元
这就是事情变得丑陋的地方。我们正在远离人们提出的简捷而有效的设计决策的空间,并进入了一个设计神经网络体系结构的算法世界。NASNet在设计理念上是令人难以置信的,但实际的体系结构是比较复杂的。我们所了解的是,它在ImageNet上表现的很优秀。
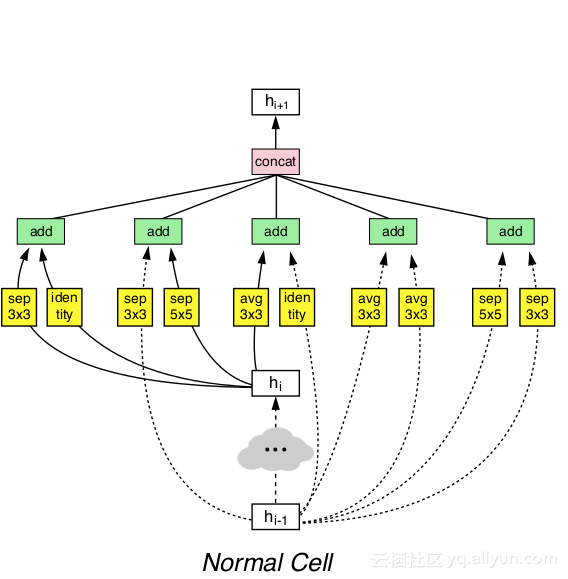
通过人工操作,作者们定义了一个不同类型的卷积层和池化层的搜索空间,每个层都具有不同的可能性设置。他们还定义了如何以并行的方式、顺序地排列这些层,以及这些层是如何被添加的或连接的。一旦定义完成,他们会建立一个基于递归神经网络的强化学习(Reinforcement Learning,RL)算法,如果一个特定的设计方案在CIFAR-10数据集上表现良好,就会得到相应的奖励。
最终的体系结构不仅在CIFAR-10上表现良好,而且在ImageNet上也获得了相当不错的结果。NASNet是由一个标准单元(Normal Cell)和一个依次重复的还原单元(Reduction Cell)组成。
defnormal_cell(x1, x2, f=32): a1 = sepconv(x1, f, k=3) a2 = sepconv(x1, f, k=5) a = add([a1, a2]) b1 = avgpool(x1, k=3, s=1) b2 = avgpool(x1, k=3, s=1) b = add([b1, b2]) c2 = avgpool(x2, k=3, s=1) c = add([x1, c2]) d1 = sepconv(x2, f, k=5) d2 = sepconv(x1, f, k=3) d = add([d1, d2]) e2 = sepconv(x2, f, k=3) e = add([x2, e2]) return concatenate([a, b, c, d, e])
这就是如何在Keras中实现一个标准单元的方法。除了这些层和设置结合的非常有效之外,就没有什么新的东西了。
倒置剩余(Inverted Residual)组块
到现在为止,你已经了解了瓶颈组块和可分离卷积。现在就把它们放在一起。如果你做一些测试,就会注意到,因为可分离卷积已经减少了参数的数量,因此进行压缩可能会损害性能,而不是提高性能。
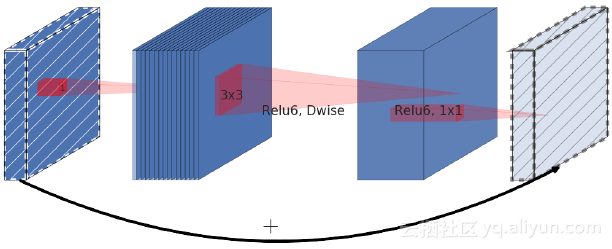
作者们提出了与瓶颈组块和剩余组块相反的想法。他们使用低成本的1x1卷积来增加通道的数量,因为随后的可分离卷积层已经大大减少了参数的数量。在把通道添加到初始激活之前,降低了通道的数量。
definv_residual_block(x, f=32, r=4): m = conv(x, f*r, k=1) m = sepconv(m, f, a='linear') return add([m, x])
问题的最后一部分是在可分离卷积之后没有激活函数。相反,它直接被添加到了输入中。这个组块被证明当被放到一个体系结构中的时候是非常有效的。
AmoebaNet标准单元
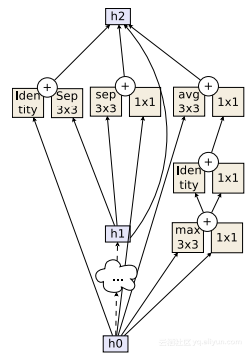
AmoebaNet的标准单元
利用AmoebaNet,我们在ImageNet上达到了当前的最高水平,并且有可能在一般的图像识别中也是如此。与NASNet类似,AmoebaNet是通过使用与前面相同的搜索空间的算法设计的。唯一的纠结是,他们放弃了强化学习算法,而是采用了通常被称为“进化”的遗传算法。但是,深入了解其工作方式的细节超出了本文的范畴。故事的结局是,通过进化,作者们能够找到一个比NASNet的计算成本更低的更好的解决方案。这在ImageNet-A上获得了名列前五的97.87%的准确率,也是第一次针对单个体系结构的。
结论
我希望本文能让你对这些比较重要的卷积组块有一个深刻的理解,并且能够认识到实现起来可能比想象的要容易。要进一步了解这些体系结构,请查看相关的论文。你会发现,一旦掌握了一篇论文的核心思想,就会更容易理解其余的部分了。另外,在实际的实现过程中通常将批量规范化添加到混合层中,并且随着激活函数应用的的地方会有所变化。